smalldatabigdreams.github.io

Small Data Big Dreams

Intro/Background

Overfitting, limited dataset sizes, and overall accuracy in machine learning are still areas rife with potential for new development today, and the ability to artificially expand training sets from existing data offers an efficient breakthrough in the field. Consequently, we explored different machine learning techniques in both tabular and image data for producing good prediction results on small data sizes while still avoiding overfitting.

Data augmentation and transfer learning have emerged as pivotal techniques in leveraging machine learning, particularly when dealing with small datasets. These techniques effectively mitigate overfitting and enhance model generalizability, working through the artificial expansion of the dataset and the strategic employment of pre-existing knowledge, respectively. This exploration aims to achieve a comprehensive application of these methodologies, along with other key strategies, to address the challenges posed by image classification and tabular regression problems on small datasets.

The implementation starts with feature selection, which involves identifying and focusing on the most relevant attributes in the dataset that significantly contribute to the predictive performance of the model. For tabular regression tasks, we first evaluated linear regression vs Random Forest as two simple models vs XGBoost and LightGBM as two more complex models. From our evaluation results, we then compared XGBoost vs Random Forest as our two main models to determine which performed best for our data at the smallest possible data size while still maintaining good RMSE and Adjusted R squared values for loss and not overfitting.

Subsequently, we then turned to data augmentation for our image data. This approach plays a crucial role in counteracting the lack of data. By creating a diverse range of transformations of the original data, we are effectively expanding the dataset and providing the model with more varied scenarios to learn from. This assists in reducing overfitting and in enhancing the model’s ability to capture desired properties and invariances.

We also leveraged transfer learning for our image data, with an aim to utilize these models’ pre-trained knowledge and fine-tune them to our specific tasks, thus making efficient use of the limited data.

Problem Statement

The motivation of this project is to experiment with various dataset sizes and methodologies for data augmentation and transfer learning processes. Data augmentation holds the promise of a powerful tool, artificially expanding training sets from existing data and thus mitigating overfitting and enhancing model generalizability. However, data augmentation today is still limited by the effectiveness of current approaches. Our goal is not simply to employ the latest models or architectures at the problem at hand, but rather to employ data augmentation, synthetic data generation, and widely used ML models for complex data and to determine the best ensemble approach to contribute meaningful insights and strategies for dealing with the challenge of small datasets.

Methods

We are going to explore different ways to deal with small datasets.

Transfer learning:

We’ll further explore how we can fine-tune existing large models for small dataset classification tasks.

• Changing all parameters of the model is probably unrealistic given our current devices.
• Add layers on top of the pre-trained model and freeze other layers.
• Use of Big Transfer model for image classification [1].

Models:

CNN (Convolutional Neural Networks): The convolution operation in a $\mathrm{CNN}$ is represented by the following equation:

In this equation:

• $I$ is the input image.
• $K$ is the kernel or filter.
• $m, n$ are the spatial coordinates in the input image.
• $h, w$ are the dimensions of the kernel.

Linear Regression

Linear Regression is represented by the following equation:

In this equation:

• $y$ is the dependent variable (target).
• $X$ are the independent variables (features).
• $\beta_0$ is the $y$-intercept.
• $\beta_1, is the coefficients of the independent variables.
• $\epsilon$ is the error term.

We created a Linear Regression model to use as a ‘control group’ in evaluating our model. This model was trained on our cleaned data and then evaluated using the Mean Squared Error(MSE) metric. The MSE value for our Linear Regression Model was 0.103 which is not too bad, but when compared to our next regression model did not match up.

Random Forest Regression

A Random Forest consists of a collection (ensemble) of decision trees. Each individual decision tree $D_i$ in the forest is built using a bootstrapped sample of the original training data, and at each node, a random subset of features is selected for splitting. The final prediction of the Random Forest regressor for a new instance $x$ is an average of the predictions of the individual trees:

In this equation:

• $Y$ is the predicted output.
• $N$ is the number of decision trees in the forest.
• $D_i(x)$ is the prediction of the $i^{\text {th }}$ decision tree for the instance $x$.

Random Forest Regression is another regression model we used that combines the principles of ensemble learning and decision tree regression. It is used for regression tasks, where the goal is to predict a continuous numerical output based on input features. Random Forest is an example of an ensemble learning method that creates multiple decision trees during the training process and combines their predictions to make the final prediction(see the image above). To build a Random Forest Regression model, multiple decision trees are constructed, each trained on a random subset of the data and a random subset of features, reducing overfitting and improving generalization. Random Forest Regression is advantageous for its robustness against overfitting, ability to handle high-dimensional data, flexibility in dealing with various data types, and built-in feature importance analysis.

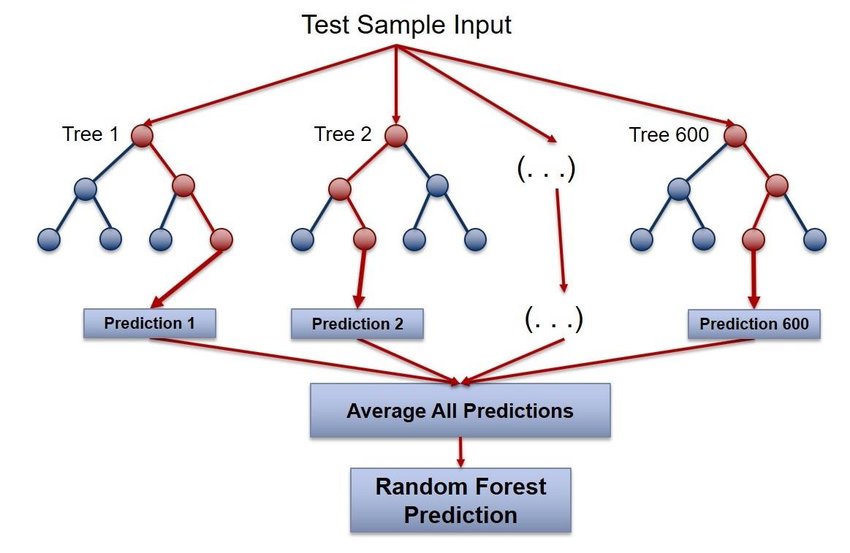
We next tested XGBoost and LightGBM due to their performance for tabular regression problems [7]. Gradient boosting is a technique used for regression and classification tasks that leverages the concept of boosting (fitting a sequence of weak learners to weighted versions of the data) to generate an ensemble of weak prediction models, in this case decision trees, to create a stronger final prediction model. It works by building the first model on the original dataset, then building additional models that focus on the instances (data points) that were incorrectly predicted by the previous models, in essence, correcting the errors of the predecessor models. The final prediction model is a weighted sum of the ensemble of models.

XGBoost (Extreme Gradient Boosting): The objective function that XGBoost optimizes is represented by the following equation:

In this equation:

• $obj(\theta)$ is the objective function to be minimized.
• $L$ is a differentiable convex loss function that measures the difference between the prediction and the target.
• $\Omega(f)$ penalizes the complexity of the model. It is defined as: $\Omega(f)=\gamma T+\frac{1}{2} \lambda|w|^2$, where $\gamma T$ is the complexity control on the number of leaves, and $\frac{1}{2} \lambda|w|^2$ is the $L 2$ regularization term on the leaf weights.
• $y$ is the target value.
• $f$ is the predicted value.

LightGBM (Light Gradient Boosting Machine): LightGBM is a gradient-boosting framework that uses tree-based learning algorithms. It is designed to be efficient and contains several advanced features, such as support for categorical features and an option for a histogram-based algorithm for bucketing continuous features. The objective function that LightGBM optimizes is represented by the following equation:

In this equation:

• $obj(\theta)$ is the objective function to be minimized.
• $L$ is a differentiable convex loss function that measures the difference between the prediction $\left(f\left(x_i\right)\right)$ and the target $\left(y_i\right)$.
• $\Omega(f)$ penalizes the complexity of the model. It is defined as: $\Omega(f)=\gamma T+\frac{1}{2} \lambda|w|^2$, where $\gamma T$ is the complexity control on the number of leaves, and $\frac{1}{2} \lambda|w|^2$ is the L2 regularization term on the leaf weights.
• $y_i$ is the target value for the $i^{\text {th }}$ instance.
• $f\left(x_i\right)$ is the predicted value for the $i^{\text {th }}$ instance.

Metrics:

We’ll use several metrics to gauge the success of our data augmentation techniques. The Fowlkes-Mallows index gauges the similarity between synthetic and original data, with a higher score signaling better augmentation. The AUC-ROC, an evaluation measure for classification problems, plots the True Positive Rate against the False Positive Rate. We anticipate improved scores with synthetic data. For multi-class models, multiple AUC-ROC curves will be generated. In tabular regression tasks, we’ll use RMSE and MAE, metrics that quantify prediction deviations from actual values, thus offering a holistic view of our prediction accuracy. We aim for these scores to also improve with the use of synthetic data [3, 4]. After the use of data augmentation, we will utilize two main scoring metrics to determine the effectiveness of the synthetic data. First, the Fowlkess-Mallows Measure utilizes the following equation:

We expect a score between 0 and 1 as well as the FM measure being higher for the data-augmented set. The second method that we will use is the “Area Under Curve” of the “Receiver Operating Characteristic” or AUC-ROC. This plots True Positive Rate (TPR) vs False Positive Rate (FPR) where:

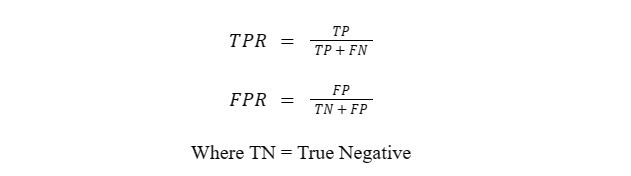
In the AUC-ROC curve, a higher value of X signifies more False positives than True negatives and a higher Y means more True positives than False negatives. The values of the AUC range from 0 to 1, where:

• 0.7 - 0.8 is acceptable
• 0.8 - 0.9 is excellent
• 0.9+ is outstanding [3]

Similarly to the FM measure, we expect the AUC-ROC to be higher for the synthetic dataset.

When using the AUC-ROC for multi-class models with N number of classes, we will plot N number of AUC-ROC curves. For example, if there are three dog breeds (A, B, and C), then we will have 1 ROC for A classified against B and C, 1 ROC for B against A and C, and 1 ROC for C against A and B.

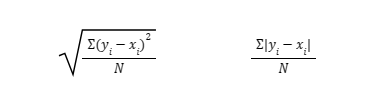
The Mean Squared Error (MSE) is calculated using the following formula:

In this equation:

• $n$ is the total number of observations.
• $y_i$ is the actual value for the $i$-th observation.
• $\hat{y}_i$ is the predicted value for the $i$-th observation.

The RMSE (Root Mean Square Error) is calculated using the following formula:

$RMSE$ = $sqrt((1/n)$ * $Σ(yi - y_hat_i)^2)$

• n is the total number of observations.
• yi is the actual value for the i-th observation.
• y_hat_i is the predicted value for the i-th observation.

The adjusted R^2 can be computed from the R^2 score using the formula:

$Adjusted$ $R^2$ = $1 - ((1 - R^2) * (n - 1)) / (n - k - 1)$

-R^2 is the coefficient of determination, which measures how well the regression predictions approximate the real data points.

• where R^2 = 1 - SS_res / SS_tot
• SS_res = the sum of squares of the residual errors.

• SS_tot = total sum of squares.

• n is the total number of observations.
• k is the number of predictors in the model.

Adjusted R^2 provides a balanced measure of model fit that takes into account the number of predictors, while RMSE penalizes large prediction errors, making it useful when it’s particularly important to minimize large mistakes.

Results

Data Cleaning

Tabular Data

Our initial path was to move forward with the Uber drivetimes data set, however, after more consideration, we changed our comparison dataset to the critical superconductor dataset as provided here: https://archive.ics.uci.edu/dataset/464/superconductivty+data. This is due to the dataset being featured as a good dataset for benchmarking due to its 82 features and 21263 rows of data.

Original Correlation Heat Map for Superconductor Data (Uncleaned):

LASSO (Superconductor):

PCA (Superconductor):

Updated Correlation Heat Map for Superconductor Data after Lasso + PCA (Cleaned):

We originally started with a data size of 81 features by 21,263 rows of data, with ‘critical temp’ being our target variable. We then performed Lasso regularization to determine our most important features given our relatively high dimensionality for tabular regression. From lasso, our data went to 14 features by 21,263 rows. We then performed PCA on this data to reduce the rows of data while still keeping most of the data variance and original information of the data via creating new, independent variables. This finally reduced our dataset size to 8 features by 14,884 rows of data for faster model building while still retaining most of the variance.

Image Data

The CIFAR-10 dataset of 60,000 labeled images belonging to 10 different classes is a popular dataset that comes with the PyTorch library. We randomly generated a smaller subset of this dataset, consisting of 1,000 images, in order to account for overfitting mitigation, balanced representation, and overall computational efficiency.

Random selection helps to ensure that the subset represents the overall distribution of classes in the original dataset. Additionally, cleaning the dataset to a much smaller subset also helps mitigate overfitting by reducing the complexity and redundancy of training data, allowing for further generalizations to larger datasets in the future.

Data augmentation:

Data augmentation methods, such as random croppings, rotations, and changing perspectives, are ways to deal with small datasets. We utilized these methods for data augmentation and will work to find which combinations of them are the optimal combo.

Control Image:

• No augmentation was performed on these images
  

Random Crop:

• Zooms into and crops a random portion of the image
  

Grayscale:

• Changes RGB values to shades of gray
  

Rotations (90, 180, and 270 degrees respectively):

• This helps the model recognize all sorts of rotated images
  

Perspective Changes (0.3 and 0.6 respectively):

• This is used to train the model for stretched and tilted images
  

Training augmented dataset result

Here are the results of training CNN on augmented datasets:

Random Crop:

Random Rotate:

Random Perspective:

Combined:

We primarily explored random crops, random rotation, and random perspective. Comparing these three, random rotation shows the best performance in overcoming the overfitting issue of a small dataset. Augmentation that combines them together shows the best performance, and there’s no overfitting issue in the final result, indicating the usefulness of augmentation in tackling overfitting problem.

Model

Image:

We use a Convolutional neural network model to perform image classification. For the model, we use 3 CNN layers with ReLU as an activation function and max-pooling after each layer. After the CNN layers, we use 2 fully connected layers to get the final classification result. For the loss function, we use cross-entropy loss.

The benchmark is the complete dataset of CIFAR10 and the model shows good performance on it:

Tabular:

We initially tested linear regression and random forest due to their simple architecture and applicability to our tabular regression dataset. After this, LightGBM and XGBoost were evaluated due to their tree-based architecture which has shown the most promise for tabular-based data [6]. Based on the results, it can be seen XGboost outperforms LightGBM perhaps due to its split finding algorithm over lightgbm’s histogram for data binning, or regularization in the objective function. It should also be noted that lightgbm typically performs better on larger datasets, and since with ~20,000 rows of data one could consider our tabular data as medium-sized, XGBoost could be considered as more suited for our current dataset [7]. From the validation graph we can also conclude that our model is currently not overfitting when trained on 70% of the full data. Based on these initial comparisons, we decided to evaluate our random forest model vs our XGBoost model to determine which would perform best on a limited dataset. Based on our results, random forest performed best across RMSE, adjusted R2, and validation error scores for the majority of sample sizes.

Random Forest Regression ultimately proved to be better performing than Linear regression as shown in the bar graph below comparing MSE values.

XGBoost performed better than LightGBM likely due to the smaller data size (14884 x 8) after data cleaning and (21263 x 82) before, which since LightGBM uses a leaf-wise growth strategy that could lead to deeper, complex trees which could lead to overfitting (thus is usually more suited for a larger dataset). Compared to XGBoost’s level-wise construction which generates more balanced trees and is less likely to overfit on smaller data.

Based on these results, we decided to move forward with XGBoost and ultimately test it vs our Random Forest model as shown below.

From the results above, it was surprising to see that random forest was actually the better model for our data mostly across the board. As can be seen from the PCA transformation, while most of the data was fairly clustered there definitely still existed some outliers which could have swayed random forest to perform better due to its bagging strategy. It should be noted though that not much time was spent on optimizing the hyperparameters of both and so if given more time, a strategy such as bayesian optimization to thoroughly investigate the optimal hyperparameter combination of both models could have led to slightly different outcomes. By ~3000 samples, both models passed the adjusted R2 score of 0.85 wile still keeping a low validation error showing they could be adequate regression models by that sample size.

Finally, it should be noted that originally GAN and Diffusion models were being explored to generate synthetic data for the dataset as another remedy for working with small sample sizes. However, this exploration was dropped after quite a bit of time attempting to get the GAN and diffusion models to work but ultimately coming up short mainly due to our predicting our target variable being a continuous regression problem while techniques such as GAN, diffusion, or other methods for increasing size via oversampling such as SMOTE (Synthetic Minority Oversampling Technique) being better suited for classification problems or discrete regression problems. Consequently, a different dataset should have been chosen from the beginning if we were to have thoroughly explored these techniques.

Transfer Learning

Image:

We fine-tune the Resnet18 model for image classification tasks. We freeze all layers of pre-trained Resnet18 model except the last output layer.

As a control group, fine-tuning Resnet on the full CIFAIR dataset works fine:

Here are the results for fine-tuning Resnet on datasets with different sizes:

300 training data, 200 testing data:

1000 training data, 500 testing data:

2000 training data, 1000 testing data:

4000 training data, 1000 testing data:

5000 training data, 1000 testing data:

More training data and testing data generally result in better performance of the model. Fewer data usually may cause overfitting issues. For example, when there are 300 training data, the validation loss is much higher than the training loss, which is an indication of serious overfitting. Generally, training data with a size of at least 4000 will be sufficient for fine-tuning Resnet18.

Timeline:

Contribution Table:

Name	Contribution
Gabe Graves	XGBoost, LightGBM, Tabular Feature Metrics/Feature Engineering, Intro, Background, Methods
Lucy Xing	Data Cleaning
Hyuk Lee	Data Augmentation
Hannah Huang	CNN and training, Transfer Learning
Rohan Nandakumar	Linear Regression, Random Forest

References:

[1] A. Kolesnikov et al., “Big transfer (BIT): General Visual Representation Learning,” Computer Vision – ECCV 2020, pp. 491–507, 2020. doi:10.1007/978-3-030-58558-7_29
[2] A. Kotelnikov, D. Baranchuk, I. Rubachev, and A. Babenko, “TabDDPM: Modelling Tabular Data with Diffusion Models”. doi: https://doi.org/10.48550/arXiv.2209.15421 Focus to learn more
[3] J. N. Mandrekar, “Receiver operating characteristic curve in diagnostic test assessment,” Journal of Thoracic Oncology, vol. 5, no. 9, pp. 1315–1316, 2010. doi:10.1097/jto.0b013e3181ec173d
[4] S. Narkhede, “Understanding AUC - roc curve,” Medium, https://towardsdatascience.com/understanding-auc-roc-curve-68b2303cc9c5 (accessed Jun. 16, 2023).
[5] “Textual inversion,” Textual Inversion, https://huggingface.co/docs/diffusers/training/text_inversion#:~:text=Textual%20Inversion%20is%20a%20technique,model%20variants%20like%20Stable%20Diffusion (accessed Jun. 16, 2023).
[6] L. Grinsztajn, E. Oyallon, G. Varoquaux, “Why do tree-based models still outperform deep learning on tabular data?”. doi: https://doi.org/10.48550/arXiv.2207.08815
[7] https://neptune.ai/blog/xgboost-vs-lightgbm